Integrale di Riemann

In analisi matematica, l'integrale di Riemann è un operatore integrale tra i più utilizzati in matematica. Formulato da Bernhard Riemann, si tratta della prima definizione rigorosa di integrale di una funzione su un intervallo a essere stata formulata.

Definizione

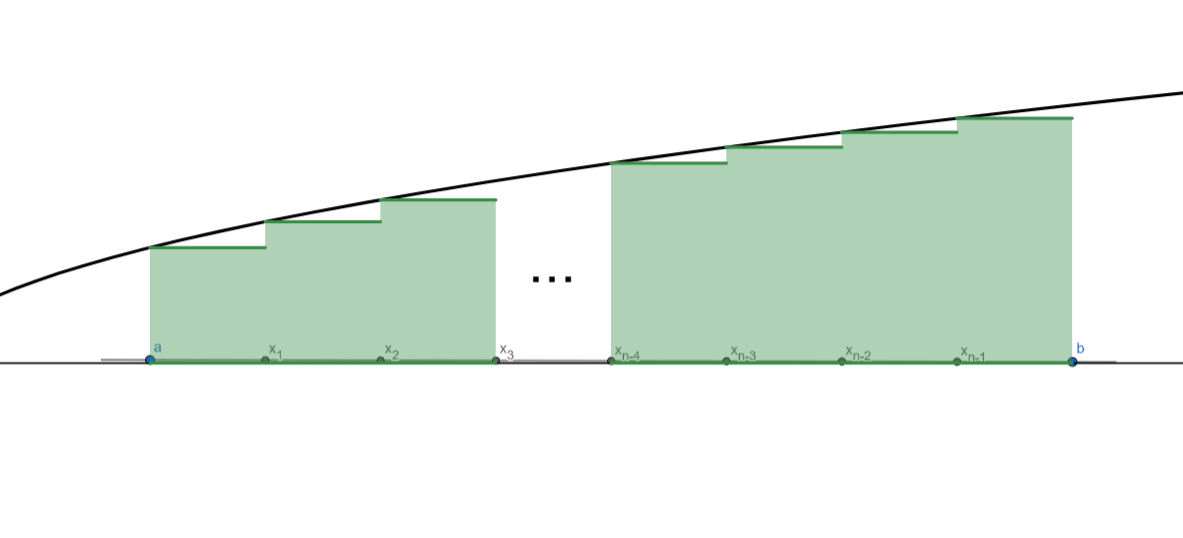
Si consideri una funzione continua ${\displaystyle f\colon [a,b]\subset \mathbb {R} \to \mathbb {R} }$, che su tale intervallo risulta limitata in virtù del teorema di Weierstrass. Si suddivida l'intervallo tramite una partizione ${\displaystyle {\mathcal {P}}=\{x_{0},\ x_{1},\ \dots ,\ x_{n-1},\ x_{n}|x_{0}=a$ in ${\displaystyle n}$ intervalli ${\displaystyle [x_{i},x_{i 1}]\subset [a,b]}$. Si definisce il calibro di una partizione ${\displaystyle {\mathcal {P}}}$ il massimo tra le ampiezze di tutti gli intervalli della partizione scelta, cioè

${\displaystyle c_{\mathcal {P}}:=\max _{i=0,\ldots ,n-1}\{x_{i 1}-x_{i}\}.}$

Per ogni intervallo ${\displaystyle [x_{i},x_{i 1}]}$ si scelga arbitrariamente un elemento ${\displaystyle t_{i}\in [x_{i},x_{i 1}]}$ e si definisca la somma di Riemann come:

${\displaystyle \sigma _{n}=\sum _{i=0}^{n-1}f(t_{i})(x_{i 1}-x_{i}).}$

Alcune scelte comuni sono

• ${\displaystyle t_{i}=x_{i},}$ in tal caso si ha una somma sinistra di Riemann;
• ${\displaystyle t_{i}=x_{i 1},}$ in tal caso si ha una somma destra di Riemann;
• ${\displaystyle t_{i}={\frac {x_{i 1} x_{i}}{2}},}$ in tal caso si ha una somma media di Riemann.

La funzione ${\displaystyle f}$ è integrabile secondo Riemann o Riemann-integrabile in ${\displaystyle [a,b]}$ se esiste finito il limite (che si dimostra non dipendere dalla scelta dei ${\displaystyle t_{i}}$):

${\displaystyle \lim _{c_{\mathcal {P}}\to 0}\sigma _{n}=:\int _{a}^{b}f(x)\,\mathrm {d} x.}$

Integrale multiplo di Riemann

Sia ${\displaystyle N\subset \mathbb {R} ^{n}}$ un dominio normale, ${\displaystyle f\colon N\to \mathbb {R} ^{n}}$ limitata e ${\displaystyle \mu }$ una misura. Sia ${\displaystyle {\mathcal {P}}=\{N_{1},\ \dots ,\ N_{k}\}}$ una partizione di ${\displaystyle N}$ in domini normali.

Si definisce la somma di Riemann-Darboux come:

${\displaystyle \sigma _{k}=\sum _{i=1}^{k}\mu (N_{i})\,{\underset {x\in N_{i}}{f(x)}}.}$

In generale la funzione ${\displaystyle f}$ è integrabile in ${\displaystyle N}$ se esiste finito il limite:

${\displaystyle \lim _{\mu (N_{i})\to 0}\sum _{i=1}^{k}\mu (N_{i})\,{\underset {x\in N_{i}}{f(x)}}=\int _{N}\!f(x)\,\mathrm {d} x_{1}\dots \mathrm {d} x_{n}.}$

Proprietà

Riemman-integrabilità e Darboux-integrabilità

In generale una funzione è Riemann-integrabile se e solo se è Darboux-integrabile, e i valori dei due integrali, se esistono, sono uguali tra loro.

Linearità

Siano ${\displaystyle f}$ e ${\displaystyle g}$ due funzioni continue definite in un intervallo ${\displaystyle [a,b]}$ e siano ${\displaystyle \alpha ,\beta \in \mathbb {R} }$. Allora:

${\displaystyle \int _{a}^{b}[\alpha f(x) \beta g(x)]\,dx=\alpha \int _{a}^{b}f(x)\,dx \beta \int _{a}^{b}g(x)\,dx.}$

Additività

Sia ${\displaystyle f}$ continua e definita in un intervallo ${\displaystyle [a,b]}$ e sia ${\displaystyle c\in [a,b]}$. Allora:

${\displaystyle \int _{a}^{b}f(x)\,dx=\int _{a}^{c}f(x)dx \int _{c}^{b}f(x)\,dx.}$

Monotonia

Siano ${\displaystyle f}$ e ${\displaystyle g}$ due funzioni continue definite in un intervallo ${\displaystyle [a,b]}$ e ${\displaystyle f(x)\leq g(x)}$. Allora:

${\displaystyle \int _{a}^{b}f(x)\,dx\leq \int _{a}^{b}g(x)dx.}$

Valore assoluto

Sia ${\displaystyle f}$ integrabile in un intervallo ${\displaystyle [a,b]}$, allora si ha:

${\displaystyle \left|\int _{a}^{b}f(x)\,dx\right|\leq \int _{a}^{b}\left|f(x)\right|\,dx.}$

Integrabilità in un sotto intervallo

Sia ${\displaystyle f\colon [a,b]\to \mathbb {R} }$ integrabile e ${\displaystyle \alpha ,\beta \in \mathbb {R} }$ tali che ${\displaystyle [\alpha ,\beta ]\subset [a,b].}$ Allora ${\displaystyle f}$ è integrabile in ${\displaystyle [\alpha ,\beta ]}$

Osservazione

Le proprietà sono state enunciate nella casistica in cui ${\displaystyle a$ Non tutte le proprietà enunciate valgono nel caso in cui gli estremi vengono scambiati ossia nel caso ${\displaystyle b$ in questa situazione molte delle proprietà enunciate necessitano un riadattamento.

Integrale di Stieltjes

Una possibile generalizzazione dell'integrale di Riemann è data dall'integrale di Riemann-Stieltjes, che rende possibile estendere la nozione di integrale utilizzando come variabile di integrazione sotto il segno di differenziale una funzione (detta integratrice):

${\displaystyle \int _{a}^{b}f\,\mathrm {d} g.}$

Se la funzione ${\displaystyle g}$ è differenziabile, vale la formula ${\displaystyle \mathrm {d} g(x)=g^{\prime }(x)\,\mathrm {d} x}$, e l'integrale di Riemann-Stieltjes coincide con quello di Riemann di ${\displaystyle fg^{\prime }}$, cioè:

${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} g(x)=\int _{a}^{b}f(x)g^{\prime }(x)\,\mathrm {d} x.}$

L'integrale di Riemann-Stieltjes è tuttavia definito anche nel caso di funzioni integratrici più generiche, che non possiedono derivata, o che sono discontinue.

L'integrale di Riemann-Stieltjes generalizza l'integrale di Riemann in maniera diversa da quello di Lebesgue, e gli insiemi delle funzioni integrabili tramite i due metodi non sono sovrapponibili. È possibile tuttavia ottenere una generalizzazione di entrambi i metodi tramite l'integrale di Lebesgue-Stieltjes.

Bibliografia

• Giuseppe Scorza Dragoni - Elementi di analisi matematica I,II, III - Padova
• Mauro Picone, Gaetano Fichera - Lezioni di analisi matematica I,II - Roma
• Jean Favard - Cours d'analyse I,II - Parigi
• Federico Cafiero - Misura di integrazione - Roma
• Mauro Picone, Tullio Viola - Lezioni sulla teoria moderna dell'integrazione - Torino
• Henri Lebesgue - Leçons sur l'intégration et la recherche de functions primitives - Parigi (1904)
• Guido Fubini - Lezioni di analisi matematica - Torino (1920)
• Ernesto Cesaro - Elementi di calcolo infinitesimale - Napoli
• Tom M. Apostol - Calcolo, Volume primo, Analisi 1 - Bollati Boringhieri
• Michiel Berstch, Roberta Dal Passo, Lorenzo Giacomelli Analisi Matematica, McGraw-Hill, Milano
• Paolo Marcellini, Carlo Sbordone Analisi Matematica Uno, Liguori Editore, Napoli, 1998, ISBN 9788820728199, capitolo 8.
• Nicola Fusco, Paolo Marcellini, Carlo Sbordone, Lezioni di Analisi Matematica Due, Zanichelli, 2020, ISBN 9788808520203, capitolo 8.

Voci correlate

• Integrale
• Integrale improprio
• Integrale di Lebesgue
• Integrale sui cammini
• Derivata
• Funzione sommabile
• Metodi di integrazione
• Passaggio al limite sotto segno di integrale

Altri progetti

• Wikiversità contiene risorse sull'integrale di Riemann
• Wikimedia Commons contiene immagini o altri file sull'integrale di Riemann

Collegamenti esterni

• Riemann, integrale di, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
• (EN) Opere riguardanti Riemann integral, su Open Library, Internet Archive.
• (EN) Eric W. Weisstein, Riemann Integral, su MathWorld, Wolfram Research.
• (EN) Riemann integral, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.
• The Integrator - Calcolo formale di primitive (Wolfram Research)
• Interactive Multipurpose Server (WIMS)